The Convolution Theorem

The convolution theorem is one of the most important relationships in Fourier theory, and in its application to x-ray crystallography. It can be stated as follows:

Consider functions a and b. Let A be the Fourier transform of a, and B be the Fourier transform of b. Then the Fourier transform of the product ab is the convolution of A and B. Call the result of this convolution C, then:

c(x) = _y a(y) b(x-y)

The product of two functions is simple - the values of the two functions are simply multiplied at every point.

The convolution of two functions is more complex. To convolute two functions, the first function must be superimposed on the second at every possible position, and multiplied by the value of the second function at that point. The convolution is the sum of all of these superpositions.

For example, here is a line, and its Fourier transform:

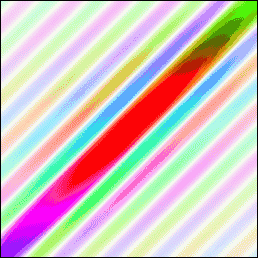
The line can be convoluted with a circle:

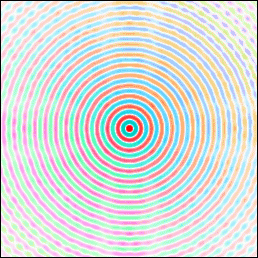
The result is a circle spread by moving it along the line, or alternatively a line spread by moving it around the circle. It is clear that the Fourier transform of the convolution is equal to the product of the transforms of the functions themselves.

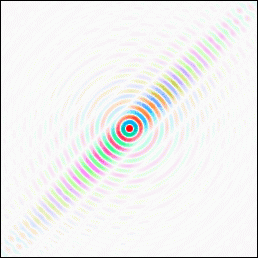
Most of the time we simply convolute one function with one or more delta-functions. If we convolute the duck with a delta function at the origin, we get back the duck at the origin.

If we convolute it with a delta-function somewhere else, then the duck is moved to that point.

If we convolute the duck with several delta-functions, we get a copy of the duck at each delta-function.