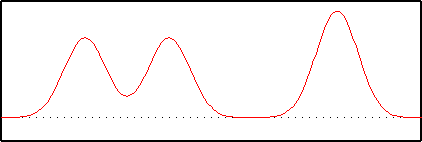
Let us consider an imaginary one-dimensional crystal. There are three atoms in the unit cell; two carbons and an oxygen. The electron density in the unit cell looks like this:

Now we will try and represent this function in terms of sine waves. The first sine wave has a frequency of 2, that is there are two repeats of the wave across the unit cell. One peak represents the oxygen, and the other the two carbons:
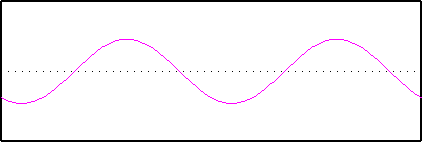
The second sine wave has a frequency of 3; three repeats of the wave across the unit cell. It has a different phase, in other words we start at a different place on the wave. The amplitude is also different:
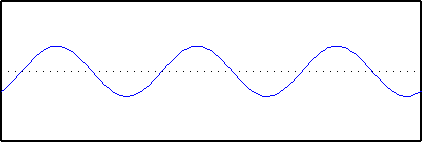
Finally, we introduce a sine wave with a frequency of 5. Two of the peaks of this wave are lined up with the carbon atoms:
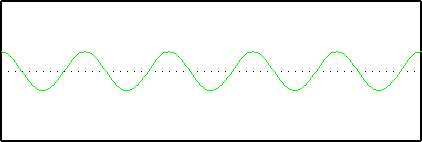
Now we add them all together:
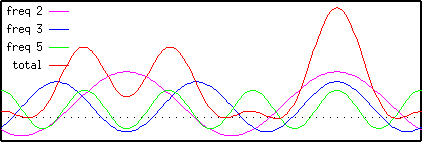
Note that the sum of the three sine-waves is a good approximation to the original unit cell. Thus we can see that the unit cell can be represented quite well using only three sine-waves, given the correct choice of frequency, amplitude and phase.
Now we will look at the Fourier Transform of the same unit cell. Note that the result consists of a series of peaks, the largest of which are at 2, 3 and 5 on the x-axis. These correspond exactly to the sine-wave frequencies which we used to reconstruct the unit cell. If you look carefully you will also see that the heights of the peaks correspond to the amplitudes of the three waves:
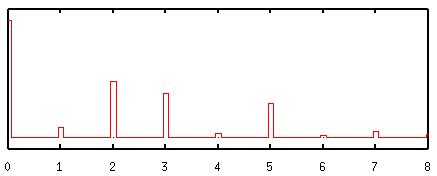
The smaller peaks in the Fourier transform correspond to additional smaller waves which would have to be added to get a perfect fit to the original density. Thus we can see that the Fourier Transform tells us what mixture of sine-waves is required to make up any function.
Of course the sine-waves go on for ever, and so there will be lots more copies of the unit cell beyond the pictures here. Also, the Fourier Transform has some other features: it has values for both positive and negative frequency, and the values are complex and not real. These features combine to determine the phase of any particular sine-wave component.