

It is possible to reconstruct an image from the Fourier magnitudes alone if we have a similar image to provide phase information. For example, suppose we are trying to reconstruct the image of a cat, and have the fourier magnitudes for it.


Since for this experiment we only have the magnitudes of the transform it is represented in monochrome, and we cannot reconstruct the image.
In addition to these magnitudes, we have an image which we know is similar to the missing cat. This image is of a Manx (tailless) cat. Since we have the image, we can calculate both the Fourier magnitudes and phases for the manx cat.


One simple method to try and restore the image of the cat is to simply calculate an image using the known Fourier magnitudes from the cat transform with the phases from the manx cat:
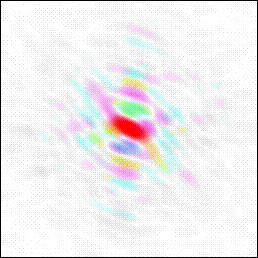

Despite the fact that the phases contain more structural information about the image than the magnitudes, the missing tail is restored at about half of its original weight. This occurs only when the phases are almost correct. The factor of one half arises because we are making the right correction parallel to the estimated phase, but no correction perpendicular to the phase (and <cos2>=1/2). There is also some noise in the image.
This suggests a simple way to restore the tail at full weight: apply double the correction to the magnitudes. An image is therefore calculated with twice the magnitude from the desired image minus the magnitude from the known image:
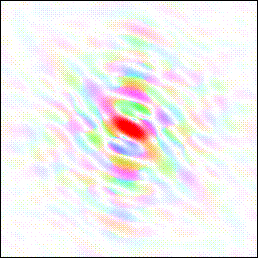

The resulting image shows the tail at full weight. However the noise level in the image has also doubled.
Often in crystallography we have an incomplete model. Thus we have observed structure factor magnitudes for a complete molecule, but a model (from which we can calculate both magnitudes and phases) for only part of it. In this case the missing potrion of the model may be reconstructed by use of the appropriate Fourier coefficients.
The first attempt to reconstruct the cat's tail above corresponds to an |Fo| map, the second to a 2|Fo|-|Fc| map.
In modern crystallography 2|Fo|-|Fc| maps have been superceded by more advances map coefficients, such as 2m|Fo|-D|Fc| (sigmaa-a) and maximum-likelihood map coefficients, but the principles are similar.
Thanks to Eric Galburt for suggesting this page.
 More Fourier transforms.
Back to the index.
More Fourier transforms.
Back to the index.