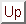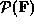 , where
, where 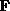 is
a vector of structure factors:
is
a vector of structure factors:


This section is based Bricogne (1984) section 4.
Our aim is to determine the joint probability distribution of structure factors, i.e. the probability of the set of all structure factors taking on a particular set of values, given some prior assumption about the distribution of atoms. From this we can generate a conditional probability distribution of some subset of structure factors given some known or assumed values of the remainder. Alternatively, we can generate a marginal probability distribution of some subset by integrating out structure factors which are unknown.
Let this joint distribution be called 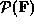 , where
, where 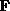 is
a vector of structure factors:
is
a vector of structure factors:
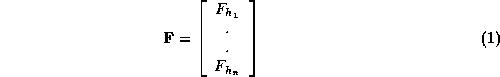
Note that given a knowledge of all the atomic positions we can
assemble 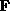 in two ways:
in two ways:
Similarly, we may consider the joint probability distribution of structure factors as a joint probability distribution of density values in a map. The probability of a particular set of structure factors (given some prior distribution of atoms) is equal to the probability of the corresponding density distribution (given the unitarity of the Fourier Transform).
For simplicity we will consider a structure containing a single atomic
type with no thermal motion, thus the structure may be represented by
a single probability distribution function of atomic coordinates
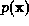 whose Fourier Transform is a set of unitary structure
factors
whose Fourier Transform is a set of unitary structure
factors 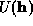 .
.
Next, we divide up the unit cell into B boxes. The probability of an
atom being placed in box j is 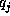 (where q is our prior estimate
of the probability distribution of atoms). A configuration of the map
can be described by the number of atoms
(where q is our prior estimate
of the probability distribution of atoms). A configuration of the map
can be described by the number of atoms 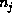 in each box. Then the
probability of a configuration is given by the number of ways a
configuration can be achieved multiplied by the probability of
generation of a certain number of atoms in each box:
in each box. Then the
probability of a configuration is given by the number of ways a
configuration can be achieved multiplied by the probability of
generation of a certain number of atoms in each box:
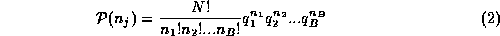
where 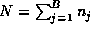 . Expanding the factorials in terms of
Stirling's formula gives:
. Expanding the factorials in terms of
Stirling's formula gives:
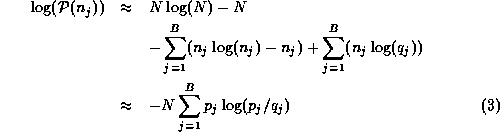
where 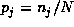 . The summation in this expression is simply the
entropy of the probability density. In the continuous form the
expressions are as follows:
. The summation in this expression is simply the
entropy of the probability density. In the continuous form the
expressions are as follows:
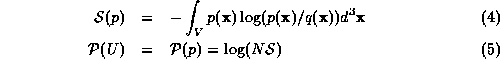
How should we construct the prior probability 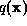 ? This
should be the most likely probability density function consistent with
whatever data is available, in other words the probability density
function with the highest probability, and therefore entropy,
consistent with any known structure factors and/or density
constraints.
? This
should be the most likely probability density function consistent with
whatever data is available, in other words the probability density
function with the highest probability, and therefore entropy,
consistent with any known structure factors and/or density
constraints.
Thus the procedure for determining the joint probability of a set of structure factors is as follows: