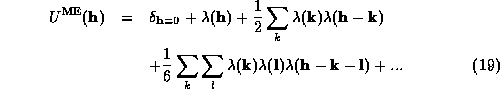

Next: Exponential Modelling
Up: Statistical Phasing: Contents
Previous: Properties of log(Z)
In the case of a uniform prior 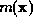 , the maximum entropy
distribution
, the maximum entropy
distribution 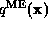 is proportional to the exponential of the
Fourier transform of the Lagrange multipliers
is proportional to the exponential of the
Fourier transform of the Lagrange multipliers 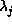 (equation
4).
(equation
4). 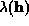 exists only for the constraint
reflections
exists only for the constraint
reflections 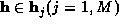 . If we therefore expand the
exponential in powers of its argument;
. If we therefore expand the
exponential in powers of its argument;
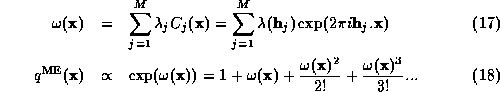
and invert for 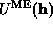 , we obtain:
, we obtain:
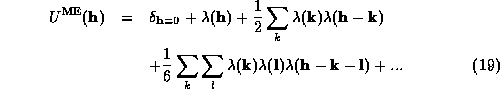
Thus we can see that the Fourier coefficients of the maximum entropy
distribution will be non-zero for the constrained reflections, plus
those reflections which are produced by triplet, quartet, and higher
combinations of reflections in the constrained set. The maximum
entropy distribution therefore makes use of the phase invariants used
in conventional direct methods.
Kevin Cowtan
Tue Oct 10 11:35:15 BST 1995
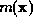 , the maximum entropy
distribution
, the maximum entropy
distribution 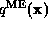 is proportional to the exponential of the
Fourier transform of the Lagrange multipliers
is proportional to the exponential of the
Fourier transform of the Lagrange multipliers 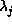 (equation
4).
(equation
4). 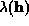 exists only for the constraint
reflections
exists only for the constraint
reflections 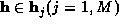 . If we therefore expand the
exponential in powers of its argument;
. If we therefore expand the
exponential in powers of its argument;


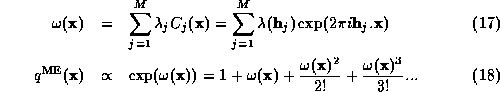
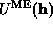 , we obtain:
, we obtain: