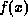 such that
such that 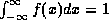 . We
define the moment generating function M(T):
. We
define the moment generating function M(T):


Let x be a random variable distributed according to the density
function 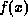 such that
such that 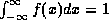 . We
define the moment generating function M(T):
. We
define the moment generating function M(T):
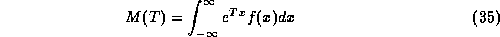
and the cumulant generating function 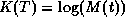 . To restore
. To restore
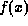 we can apply the Fourier inversion formula as follows:
we can apply the Fourier inversion formula as follows:
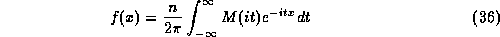
Let 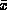 be the mean of n independent x's. Its density
function
be the mean of n independent x's. Its density
function 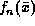 is therefore:
is therefore:
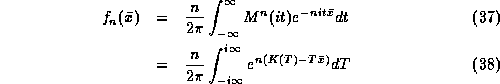
By Cauchy's theorem the value of the integral is unchanged if we integrate along any line parallel to the imaginary axis, i.e.
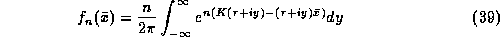
To evaluate the integral we will expand the contents of the
exponential as a power series in y about 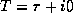 .
.
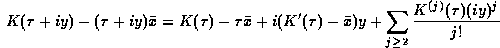
Then:
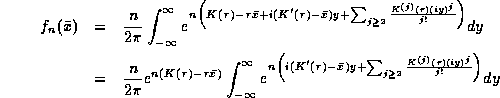
Next, we separate the first two terms in the exponential, and then expand the remaining terms as a product of power series:
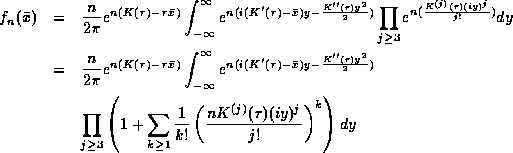
Multiplying out the product of summations, we get:
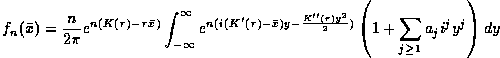
We now apply the standard integral, true for 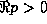 :
:
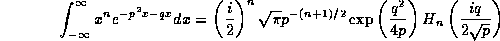
where 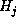 is the Hermite polynomial of degree j. Thus:
is the Hermite polynomial of degree j. Thus:
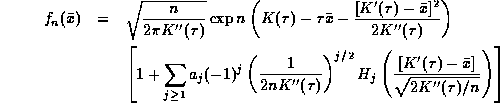
Note 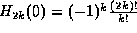 ,
, 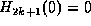 . It is not
clear that the first term dominates either the highest or lowest order
contributions to
. It is not
clear that the first term dominates either the highest or lowest order
contributions to 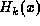 (the formal proof of convergence requires a
number of other results). However, when
(the formal proof of convergence requires a
number of other results). However, when 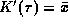 , the
arguments of the Hermite functions become zero, thus all odd orders
disappear and only the constant terms of even orders contribute. It
is certainly reasonable that this should be the best estimate to the
integral.
, the
arguments of the Hermite functions become zero, thus all odd orders
disappear and only the constant terms of even orders contribute. It
is certainly reasonable that this should be the best estimate to the
integral.
The approximation
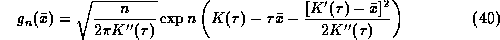
when  is chosen such that
is chosen such that  is called the
Saddlepoint approximation to
is called the
Saddlepoint approximation to 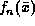 .
.