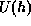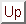
The Karle-Hauptman matrix of a set of unitary structure factors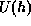 
can be defined as follows,
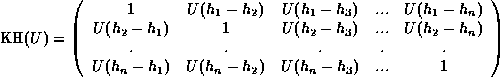
or,
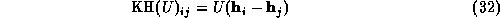
where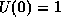 
, and conventionally 
.
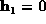Consider the product of two Karle-Hauptman matrices of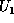 
and
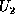, where 
.
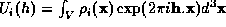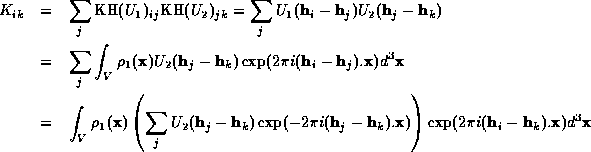
If enough reflections are included in the Karle-Hauptman determinant, the
summation over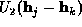 
becomes the Fourier inversion formula
for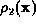 
, thus:
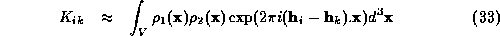
If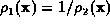 
, then:
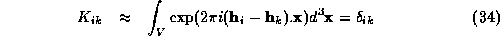
i.e.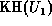 
is the inverse of 
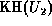. Thus, if enough terms
are included, the Karle-Hauptman matrix associated with the inverse of
an electron density function is the inverse of the Karle-Hauptman
matrix associated with the electron density function itself.