Clipper: Developing using Reflection Data

Understanding HKL_info and HKL_data<>

Storage of reciprocal space data in Clipper involved two objects: HKL_info and HKL_data<>. The first stores a list of reflections (HKLs), and the second stores a list of data of some type for each reflection.

Why is this division made? Because often, many types of data will be stored for the same reflection list, and duplicating the list of reflections for each data list would be wasteful. The relationship of an HKL_info object and several HKL_data<> objects is shown below.

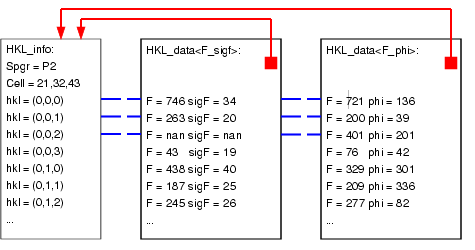
These objects handle all the crystallographic symmetry operations associated with storing data in reciprocal space. To the programmer, the data appears to fill a sphere of reciprocal space. However, only a unique set of data is stored, and any changes to a data values are automatically reflected in the symmetry and Friedel related reflections.

The HKL_info object

The HKL_info object stores a list of reflections, transformed into a standard reciprocal space asymmetric unit. For example:

P1: data is stored for l>0 or (l=0 and (h>0 or (h=0 and k>=0)))
P2: data is stored for k>=0 and (l>0 or (l=0 and h>=0))
P212121: data is stored for h>=0 and k>=0 and l>=0

However, the programmer should never need to know which asymmetric unit is being used, as data in other parts of reciprocal space are generated automatically.

The HKL_info object also stores a lookup table, which is used to rapidly determine the location in the list of a given HKL. It also stores lookup tables for the reflection class (HKL_class) and resolution (invresolsq).

The reflection list depends upon the spacegroup (which determines the reciprocal asymmetric unit and systematic absences), the cell parameters, and the resolution limit. Therefore to initialise an HKL_info object, objects of types Spacegroup, Cell and Resolution are passed to the constructor or initialiser.

Reflection classes

The 'class' of a reflection is a function of its HKL and the spacegroup, and describes whether it is centric, systematically absent, and what its allowed phase and symmetry enhancement factor or multiplicity are (i.e. epsilon). The class of a reflection is described by the class clipper::HKL_class.

Reflection resolution

The resolution of a reflection is a function of its HKL and the unit cell parameters. It is generally handled in terms of the inverse resolution squared, or 'invresolsq'. This is equal to 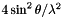$4\sin^2 \theta / \lambda^2$ .

The HKL_data<> object

The data object is not much more than an array of data, but it has a number of special methods to make crystallographic operations on that data more convenient. It is defined as a template class, where the template type is the type of crystallographic information to be stored in the object. It simply stores a list of data of that type, and a pointer to the parent HKL_info object, which defined the HKL for each element in the list. Additionally a pointer to a Cell object is stored, which may optionally be used for the case where different data comes from slight different unit cells (e.g. RT and frozen data). Therefore to initialise an HKL_data object, an HKL_info object and optionally a Cell object are passed to the constructor or initialiser.

Data types typically include several values. Examples include measured X-ray intensity and its standard deviation (I_sigI), structure factor magnitude and phase (F_sigF), and Hendrickson-Lattman coefficients (ABCD). Data types are derived from a base type (Datatype_base), and should override all the methods of that type. This will allow the data to be automatically transformed about reciprocal space, and imported or exported to a file, as required.

Methods are provided to access the data by index or by HKL. Any transformations which must be applied to the data in obtaining a symmetry or Friedel related value are applied automatically.

In order to use the class efficiently, some important difficulties must be borne in mind.

A problem arises when we wish to apply some transformation to the values stored in a data list. In this case, we must access every unique value in the asymmetric unit once and once only, applying the desired transformation. Only then will the entire data list have been transformed correctly.

A second problem arises if we want to access the stored value of the data at some position in reciprocal space, for example to expand to a lower spacegroup. Then it is necessary to search through all the symmetry operators, applying each one in turn to the desired HKL to find the operator which brings the HKL into the stored asymmetric unit, with a Friedel inversion if necessary. Clearly this can be time consuming, especially if there are many symmetry operators.

Both these problems are addressed by the use of HKL reference types. These come in two forms:

index-like references (clipper::HKL_info::HKL_reference_index)
coordinate-like references (clipper::HKL_info::HKL_reference_coord)

The index-like reference behaves like an index: it stores a reference to an HKL_info object and a position in the reflection list. It is used to loop over all the values in the reflection list, using the HKL_info::first(), and HKL_reference_index::last() and HKL_reference_index::next() methods. The HKL corresponding to the index, its resolution, and reflection class can be returned at any point.

The coordinate-like reference behaves like an HKL coordinate: it stores a reference to an HKL_info and an HKL. However to enhance performance it also stores the position in the list corresponding to that HKL, and the number of the symmetry operator used to get back into the stored asymmetric unit, along with a flag to signify Friedel inversion. Since reflections are usually accessed systematically, the next HKL used will commonly require the same symmetry operator, and so that operator is tried first. Methods are provided for incrementing and decrementing along the h, k, and l directions.

The differences between the index-like and coordinate-like reference types can be summarised as follows:

index-like types can only refer to the position of a stored datum, i.e. reflection in this list.
coordinate-like types can refer to any possible position, and therefore also store the symmetry transformations required to get back to the stored data.

HKL reference types may be shared between any data lists which have the same reflection list. It is the responsibility of the programmer to ensure this restriction is obeyed.

HKL_data code fragments

Importing and exporting HKL_data

Currently objects are provided for import and export to CCP4 '.mtz' files and XtalView/SHELX '.phs' files. (More will be added later).

To import a datalist from an MTZ files we need an HKL_info object to hold the reflection list and an HKL_data object to hold the actual data. We also need MTZdataset and MTZcrystal objects to hold the additional information which will be returned from the MTZ file. Then we create a CCP4MTZfile object, open it onto a file, and read the reflection list and data.

  clipper::HKL_info myhkl;            // define objects
  clipper::MTZdataset myset;
  clipper::MTZcrystal myxtl;
  clipper::HKL_data<clipper::data32::F_phi> fphidata( myhkl, myxtl );

  clipper::CCP4MTZfile mtzin;
  mtzin.open_read( "my.mtz" );        // open new file
  mtzin.import_hkl_info( myhkl );     // read sg, cell, reso, hkls
  mtzin.import_hkl_data( fphidata, myset, myxtl, "native/CuKa/[FCAL PHICAL]" );
  mtzin.close_read();

Similar functions are used for accessing XtalView/SHELX .phs files, although the interface is much simpler since these files do not contain labelled data.

Expanding reflection data to a lower symmetry

To expand a list of data to a lower symmetry, we need two reflection lists, one for each spacegroup; and two datalists, one for each reflection list. The lower symmetry list is then filled by looping over all the reflections in that list an requesting the value from the other list for that HKL.

  clipper::HKL_info oldhkl( .... );
  clipper::HKL_data<clipper::data32::f_phi> olddata(oldhkl);
  // ---- fill the objects here ----
  clipper::HKL_info newhkl( Spacegroup( Spgr_descr( 1 ) ),
                            oldhkl.cell(), oldhkl.resolution() );
  clipper::HKL_data<clipper::data32::f_phi> newdata(oldhkl);
  HKL_info::HKL_reference_index ih;
  for ( ih = newhkl.first(); !ih.last; ih.next() ) {
    newdata[ih] = olddata[ih.hkl()];
  }

Note that the '.hkl' is vital, as we want the data with the corresponding hkl, not the data from the corresponding position in the list. If efficiency is paramount, using an HKL_reference_coord to access the old list will save some searches over the symmetry operators:

  clipper::HKL_info::HKL_reference_index ih;
  clipper::HKL_info::HKL_reference_coord ik( oldhkl );
  for ( ih = newhkl.first(); !ih.last; ih.next() ) {
    ik.set_hkl( ih.hkl() );
    newdata[ih] = olddata[ik];
  }

Applying simple operations to a whole data list

While it is simple to loop through a reflection list and apply some transformation on the data, some simple operations have been automated using built-in C++ arithmetic operators for data of specific types, logical operators for data or any type, comparison operators for flags, and function 'Computation operators' for more complex operations.

Arithmetic operators.

Arithmetic operators are defined for the addition, subtraction, and scaling of map coefficients (i.e. HKL_data<datatypes::F_phi>), and for the addition and scaling of Hendrickson-Lattman coefficients (class HKL_data<datatypes::ABCD>). Thus, to add two lists of map coefficients, the following code is required:

  clipper::HKL_data<clipper::data32::F_phi> fphi1, fphi2, fphi3;
  // ---- set data here ----
  fphi3 = fphi2 + fphi1;

The columns are added using vector addition. If any values in either list are missing, then the result is missing. Subtraction is similar. Multiplication by a scalar scales the magnitude of every non-missing element in the list.

Logical operators.

Standard C/C++ bitwise logical operators (&, |, ^, !) may be applied to any data list. For each data in the list, the value 'true' will be returned if the data is not missing, or false if it is missing. The result of the operation is a new data list of type HKL_data<Flag_bool>, containing the results of the logical operation. This may be used in further logical operations, or may be used as a mask to eliminate data from a list using the HKL_data::mask() method.

Comparison operators.

Comparison operators (==, !=, >, <, >=, <=) may be applied to a data lists of flags (i.e. HKL_data<datatypes::Flag>), to compare the values in the list with a single integer. This is commonly used in the handling of Free-R test sets. The result is a list of HKL_data<Flag_bool>, where the value of the flag for each reflection is the result of the compraison of the frag for that reflection and this given integer. So, for example, to make a list of data containing only the values for which the test set is numbered 18 or greater, use the following code:

  clipper::HKL_data<clipper::data32::F_sigF> fsigf, fsigftest;
  clipper::HKL_data<clipper::data32::Flag> flag;
  // ---- set data here ----
  fsigftest = fsigf;
  fsigftest.mask( flag >= 18 );

Computation operators

Computation operators handle more complex crystallographic tasks, and will be discussed in more detail.

To use a computation operator, call the compute() method of the destination datalist. This method must be supplied with one or two source datalists, and a computation operator. This is an object which performs the computation for an individual reflection, and is usually constructed on the fly.

Some computation operators simply convert a datalist of one type to a datalist of another type. For example, you can convert a phase and weight to Hendrickson Lattman coefficients. (Of course C and D will be 0, because a phase and weight can only describe a unimodal distribution).

  clipper::HKL_data<clipper::data32::Phi_fom> myphifom;
  // ---- set data here ----
  clipper::HKL_data<clipper::data32::ABCD> myabcd;
  myabcd.compute( myphifom,
    clipper::data32::Compute_abcd_from_phifom() );

Some computation operators take data from two datalists. For example, you can calculate map coefficient (magnitude and phase) from a set of observed magnitudes and a phase and weight:

  clipper::HKL_data<clipper::data32::F_sigF> myfsig;
  clipper::HKL_data<clipper::data32::Phi_fom> myphifom;
  // ---- set data here ----
  clipper::HKL_data<clipper::data32::F_phi> myfphi;
  myfphi.compute( myfsig, myphifom,
    clipper::data32::Compute_fphi_from_fsigf_phifom() );

Computation operators may operate on a datalist itself, and can also take parameters. These parameters are passed to the constructor of the computation operator. For example, to apply a scale factor of 2.0 and and U-value of 0.5 to a list of reflections, use the following code:

  clipper::HKL_data<clipper::data32::F_sigF> myfsig;
  // ---- set data here ----
  myfsig.compute( myfsig,
    clipper::data32::Compute_scale_u<data32::F_sigF>( 2.0, 0.5 ) );

Computation operators are provided for performing addition, subtraction and scaling of map coefficients (i.e. F_phi), addition and computation of Hendrickson Lattman coefficients, and for scaling data. It is fairly simple to define new computation operators, see core/hkl_compute.h.

Defining a new reflection datatype

Several data types are defined in the file hkl_datatypes.h . Defining a new type proceeds as follows:

Define a struct containing the data which needs to be stored for each reflection. A default constructor should be supplied which initialises all the data to NaN for floats, or an illegal value for ints (e.g. -1 for Free-R flag).
Defined a member function `void friedel()' which changes the values of the data to the values of the Friedel opposite of the data. (e.g. a magnitude is unchanged, a phase will be negated).
Defined a member function `void shift_phase(const float)' which chages the values of the data to the value of a symmetry equivalent with the given phase shift from the original. (e.g. a magnitude is unchanged, a phase will have the shift added to it).
Define a member function `static const string type()' for that struct which returns a `type name' string for this type. This is used to identify the data type and to infer column names in an mtz file.

For example, an F_phi group are defined as follows:

struct F_phi
{
  float f,phi;
  F_phi() { f=phi=Nan(); }
  static const String type() { return "F_phi"; }
  void friedel() { phi=-phi; }
  void shift_phase(const ftype dphi) { phi+=dphi; }
  const bool missing() const { return (isnan(f) || isnan(phi)); }
};

The datalist types are constructed from the individual data type by a template class.

If you need to store your new datatype in an MTZ file, you must also define an MTZ_iotype by derivation from clipper::MTZ_iotype_base, create a static instance of the new MTZ_iotype, and add it to the mtz_iotype_registry.